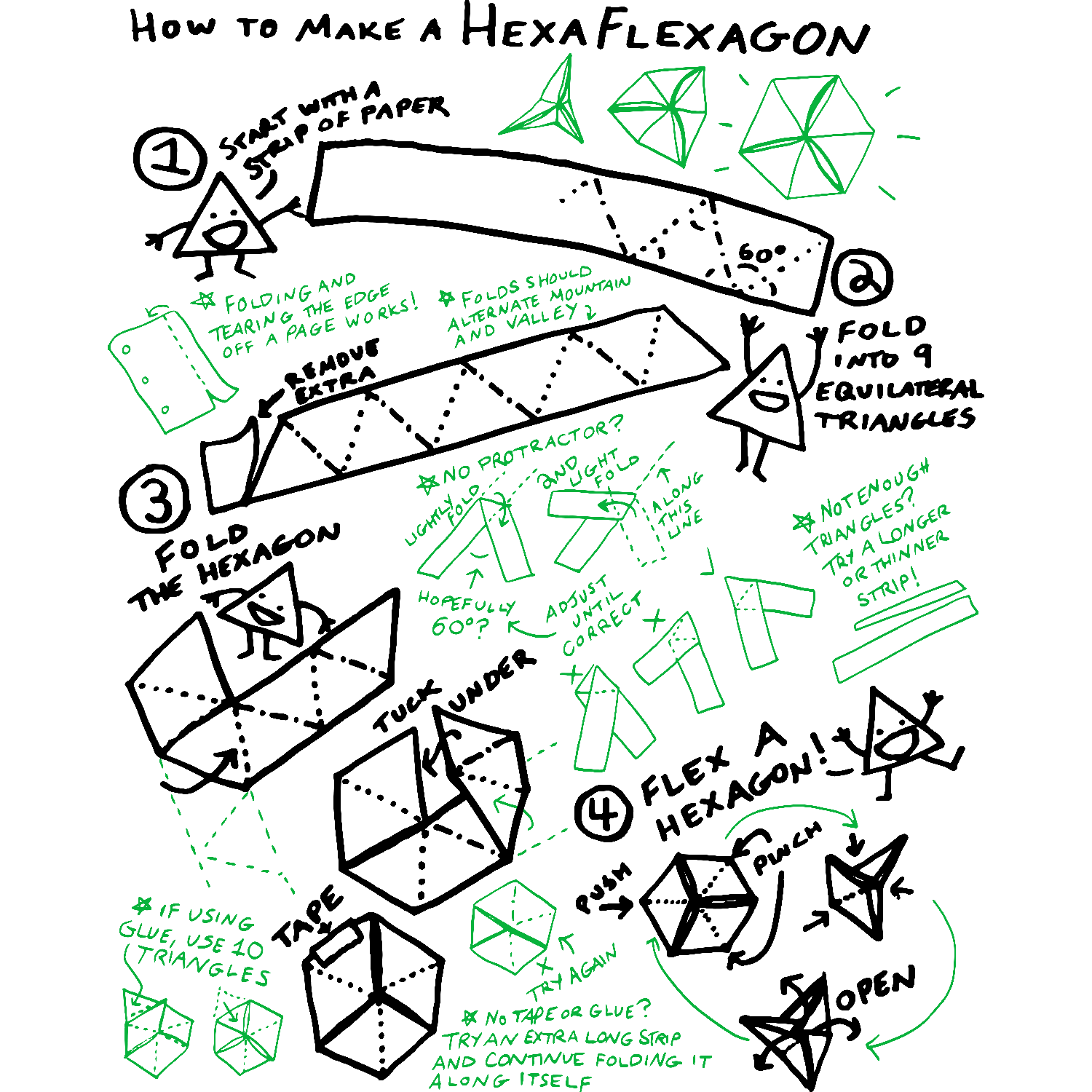
oh, hexaflexagons. one of my favourite dimension-bending paper fidgets. ever since i watched the hexaflexagon series by (the one and only) Vi Hart way back when, i've been obsessed with making these things, especially in elementary school. trihexaflexagons, hexahexaflexagons, even tetraflexagons (? we dont talk about tetra). like how i taught people back them, im going to teach you guys!!!!!! :DDDD
So say you just moved from England to the US and you've got your old school supplies from England and your new school supplies from the US and it's your first day of school and you get to class and find that your new American paper doesn't fit in your old English binder. The paper is too wide, and hangs out. So you cut off the extra and end up with all these strips of paper. And to keep yourself amused during your math class you start playing with them. And by you, I mean Arthur H. Stone in 1939. Anyway, there's lots of cool things you can do with a strip of paper. You can fold it into shapes. And more shapes. Maybe spiral it around snugly like this. Maybe make it into a square. Maybe wrap it into a hexagon with a nice symmetric sort of cycle to the flappy parts. In fact, there's enough space here to keep wrapping the strip, and then your hexagon is pretty stable. And you're like, "I don't know, hexagons aren't too exciting, but I guess it has symmetry or something." Maybe you could kinda fold it so the flappy parts are down and the unflappy parts are up. That's symmetric, and it collapses down into these three triangles, which collapse down into one triangle, and collapsible hexagons are, you suppose, cool enough to at least amuse you a little bit during your class. And then, since hexagons have six-way symmetry, you decide to try this three-way fold the other way, with flappy parts up, and are collapsing it down when suddenly the inside of your hexagon decides to open right up. What? You close it back up and undo it. Everything seems the same as before, the center is not open-uppable. But when you fold it that way again, it, like, flips inside-out. Weird. This time, instead of going backwards, you try doing it again. And again. And again. And again. And you want to make one that's a little less messy, so you try again with another strip and tape it nicely into a twisty-foldy loop. You decide that it would be cool to color the sides, so you get out a highlighter and make one yellow. Now you can flip from yellow side to white side. Yellow side, white side, yellow side, white side Hmm. White side? What? Where did the yellow side go? So you go back, and this time you color the white side green, and find that your paper has three sides. Yellow, white, and green. Now this thing is definitely cool. Therefore, you need to name it. And since it's shaped like a hexagon and you flex it and flex rhymes with hex, hexaflexagon it is. That night, you can't sleep because you keep thinking about hexaflexagons. And the next day, as soon as you get to your math class you pull out your paper strips. You had made this sort of spirally folded paper that folds into again, the shape of a piece of paper, and you decide to take that And use it like a strip of paper to make a hexaflexagon. Which would totally work, but it feels sturdier with the extra paper. And you color the three sides and are like, Orange, yellow, pink. And you're sort of trying to pay attention to class. Math, yeah. Orange, yellow, pink. Orange, yellow, white? Wait a second. Okay, so you color that one green. And now it's orange, yellow, green. Orange, yellow, green. Who knows where the pink side went? Oh, there it is. Now it's back to orange, yellow, pink. Orange, yellow, pink. Hmm. Blue. Yellow, pink, blue. Yellow, pink, blue. Yellow, pink, huh. With the old flexagon, you could only flex it one way, flappy way up. But now there's more flaps. So maybe you can fold it both ways. Yes, one goes from pink to blue, but the other, from pink to orange. And now, one way goes from orange to yellow, but the other way goes from orange to...neon yellow. During lunch you want to show this off to one of your new friends, Bryant Tuckerman. You start with the original, simple, three-faced hexaflexagon, which you call the trihexaflexagon. And he's like, whoa! and wants to learn how to make one. And you're like, it's easy! Just start with a paper strip, fold it into equilateral triangles, and you'll need nine of them, and you fold them around into this cycle and make sure it's all symmetric. The flat parts are diamonds, and if they're not, then you're doing it wrong. And then you just tape the first triangle to the last along the edge, and you're good. But Tuckerman doesn't have tape. After all, it was invented only 10 years ago. So he cuts out ten triangles instead of nine, and then glues the first to the last. Then you show him how to flex it by pinching around a flappy part and pushing in on the opposite side to make it flat and trianglly, and then opening from the center. You decide to start a flexagon commitee together to explore the mysteries of flexagation. But that will have to wait until next time.
So say you're Arthur Stone, and you're showing your hexaflexagon to your friend, Tuckerman, and you've already blown his mind by showing him it has three sides-- orange, yellow, pink, orange, yellow, pink-- but now you're about to extra super blow his mind by showing him that there's even more colors. And he's like, whoa, where did the blue side come from? But you're having trouble finding all six. Like, you know there's a green side somewhere in here, but where is it? You're all like, OK, Tuckerman, I think I found the green side. It's right in here. Anyway, Tuckerman immediately decides he needs to discover the fastest way to get to all the colors, which he calls the Tuckerman traverse. So you and Tuckerman are working on that, and there's hexaflexagons all over the lunch table, and another student is curious about what you're doing and wants to join your committee. His name is Richard Feynman. So stop being Arthur Stone, and start being Brian Tuckerman. So you're Tuckerman, and you teach Feynman how to make the hexa-hexaflexagon by first folding a strip of 18 triangles with the 19th for gluing. You and Stone have just figured out how to number the faces before you fold them by dissecting a perfect specimen. You number them 1-2-3, 1-2-3, 1-2-3, 1-2-3, 1-2-3, 1-2-3. Glue on one side. Flip it, and glue 4, 4, 5, 5, 6, 6, 4, 4, 5, 5, 6, 6, 4, 4, 5, 5, 6, 6 on the other. You coil it around so that you get ones and twos and threes on the outside like 1, 2, 2, 3, 3, 1, 1 2, 2, 3, 3, and then fold that around into a hexagon, so that all the twos are on the front. And then flip it, and glue the two blue parts together, so that all threes are on the back. Feynman has some trouble flexing it, but you show him how to pinch two triangles together and then push in the opposite side. He somehow still does it wrong and ends up doing it backwards, flexing in reverse. Now he's all intrigued by all the flexing possibilities, and you're like, let me show you the Tuckerman traverse. But Feynman, being Feynman, is like, we must create a diagram. And Tuckerman's like, really, it's not that hard. No, diagram. So you're Feynman, and you've already seen you can cycle from one to two to three, one, two, three. So you write that down with arrows and stuff. Or you can go backwards, but from one, two, and three, you can also flex the other way, in which case one goes to six, or two to five, or three to four. And if you did one to six, once you're at six, you can only flex one way, because the other doesn't work. You have to go to three or backwards back to one. But then you notice that if you go to three, you can only flex one way, and the other is un-open-up-able. But before when you were on three, you could go either to one or four, but now you can only go to one. And you can go backwards to six, but not backwards to two, which means that this three isn't the same three as the first three. Somehow it's the same color, but in a different state. You show this to your friend John Tukey, and he's like, oh yeah, that makes sense. And he draws a star in the middle of your three and sits back as if that explained everything. So you're like, whatever, and flip it back around to get to the other three and check it. The star turns into a not star. And from this alternate three, there's this 1-6-3 loop that connects to the main loop at one, which is the same one as one has always been. But there's a different one off of the main two in the 2-5-1 loop. And of course, everything looks different if you flip it over. And these threes are also different, because they have different numbers on the other side. And you complete a diagram of possibilities, which allows you to find the optimal Tuckerman traverse. You also diagram the original trihexaflexagon, which is pretty simple. The flexagon committee approves your diagrams and decides to call them Feynman diagrams. Everything is going great until 1941, because suddenly there's important war stuff to do, and flexagons are largely forgotten. OK. Now fast forward 15 years, and be Martin Gardner. You're an amateur magician, and you're hanging out at your friend's place talking about magician stuff. Anyway your friend shows you something you've never seen before-- a big flexagon he's made out of cloth. And you're thinking, hey, this is awesome. Maybe other people would like to know about this flexagon thing. So you write an article for Scientific American, and soon you've landed yourself a gig writing a regular column about recreational mathematics called "Mathematical Games," and it's a huge success and gets hundreds of comments. I mean, letters, and there's nothing else like your column. And all the cool people are inspired by you, and you're pretty much the reason why people know about things like tangrams, and Conway's Game of Life, and the work of MC Escher, and other things like that. Now fast forward 50 years, and say you're me in the generation of people inspired by Martin Gardner are now the people inspiring you. So he's your math inspiration grandfather. And now you yourself are in the business of mathematically inspiring people, and you want them to be aware of their math inspiration heritage. OK, now say you are you. If you think hexaflexagons are cool that was just column number one. And I invite you to join in with the hundreds of people to celebrate Martin Gardner's birthday every October 21. This year, there will be hexaflexagon parties in homes and schools all over the world. And if you want to attend or host one, check the description. I'm celebrating by making these videos, and also I just like the image of flexagons everywhere-- floating around lunch tables, spilling out of your pockets, lost in your couch cushions. I like to keep some ready to deploy out of my wallet or tiny yellow purse, in case of a flexagon emergency. And then there's more recent innovations in flexagon technology, and all the cool ways to color them, and other stuff. But that will have to wait until next time.
(apologies for inconsistencies i literally just went copy paste)
So back in the day we had to make our own fidget toys, and to make a hexaflexagon all you need is 30 seconds and a scrap of paper if you know how, which is probably why this is my #1 most requested video so today I’m gonna show you my hexaflexagon techniques. Now the goal is to be able to create one instantly anytime anywhere without scissors tape or glue but to build your hexaflexaskills you can start with a printable pattern such as this one. The essence of a hexaflexagon is 9 triangles in a twistyloop and you can use 10 triangles if you glue the last to the first or use 9 if you’re using tape. Having a pattern is helpful for folding perfect equilateral triangles and also it’s easier to fold the finished shape if you have your mountains and valleys in a row, dotted lines are valley folds and dashed lines are mountain folds, and you can check that all your triangles are happy and accurate by folding them back and forth on top of each other and seeing that they all line up. The #1 place people go wrong is when folding and taping the loop together, and here’s where the mountain folds can help you do it right. It is of vital importance that the three flappy bits be symmetrically arranged all triangly-like. If you’ve got a flappy flap that goes all the way straight across the hexagon or two flappy bits right next to each other, just try again. Then finally, tape the first and last triangle together around the edge, or sometimes you’ll get a case where you tape them across the side, or if you’re using glue then just flap that flap on over and glue that whole 10th triangle to the first triangle, just try not to accidentally tape or glue together anything else. If your creases are strong, they will guide you in the hexaflexagon’s construction and also in its use, where you pop up the center and pinch the sides together in a three-fold way and open it up from the center. The great thing about hexaflexagons is that aside from their figitability they also offer an opportunity for doodling, drawing, and derocating, and here’s where this more robust fold-over design can help, especially if you have markers that bleed through your paper. It’s also a great way to hide the template lines after you’ve made your creases. And once that’s together you can color both sides however you want to, and also the third side however you want to. Ok so once you have a feel for that, it’ll be easier to do it without the pattern or scissors. The first trick is getting a nice even strip of paper, which you can do by folding the edge off a page and making sure the edge lines up on both sides, creasing firmly, and I like to crease back and forth a couple times so that it tears off without too much trouble. Now here’s what some consider the hardest part: getting your first triangle, which means getting a perfect 60-degree angle. If you have any equilateral triangles around you can just copy off of them but if not, here’s what you do: first fold your best guess and crease only very lightly, then lightly fold along the edge and see if things line up. When they do line up, you should be able to see the trianglyness of your folds. But they probably won’t line up the first time, and so you adjust back and forth until it does. When you get a feel for it, you should be able to do most of the adjusting while you’re making your first creases, it just takes a little practice. You can also work on your triangle folding skills by using a pattern but pretending there’s no pattern. Ok so the great thing about 60-degree angles is that once you’ve got one, they self-replicate, you can keep folding along the lines and just try and keep it so that the edges line up and the corners line up as much as possible. And you only need 9 triangles so remove the extra and you’re ready to go. And going freehand you might end up with the twistyloop connecting at the edge or in the middle and it could be right-handed or left-handed, it’s all good. A major pitfall of hexaflexigation is not getting enough triangles because your strip is too wide for its length. When you’re decorating you might get that bleed-through problem again but you can start with a doubled-over strip of paper and you’re ready for arts, I’m gonna do leaves and a flower and roots, check it out. Ooh or you could put secret notes in the middle, so secret. If you have no tape or glue you can keep the strip extra long and wrap it around extra, and if you flexigate with precision and control you can keep the ends from flapping out, or maybe it falls apart and you have to fold it back together. And then finally, once you really get a feel for things, you can take any scrap of paper and turn it into a strip without needing to cut or tear, you just fold everything in, and you can even skip some of the triangly preparation and instead add the missing creases as you flex it the first few times. Anyway those are my tricks and if you want free patterns they are at vihart.com/hexaflexagons But practice your hexaflexagon skills because you will need them next month, stay tuned.

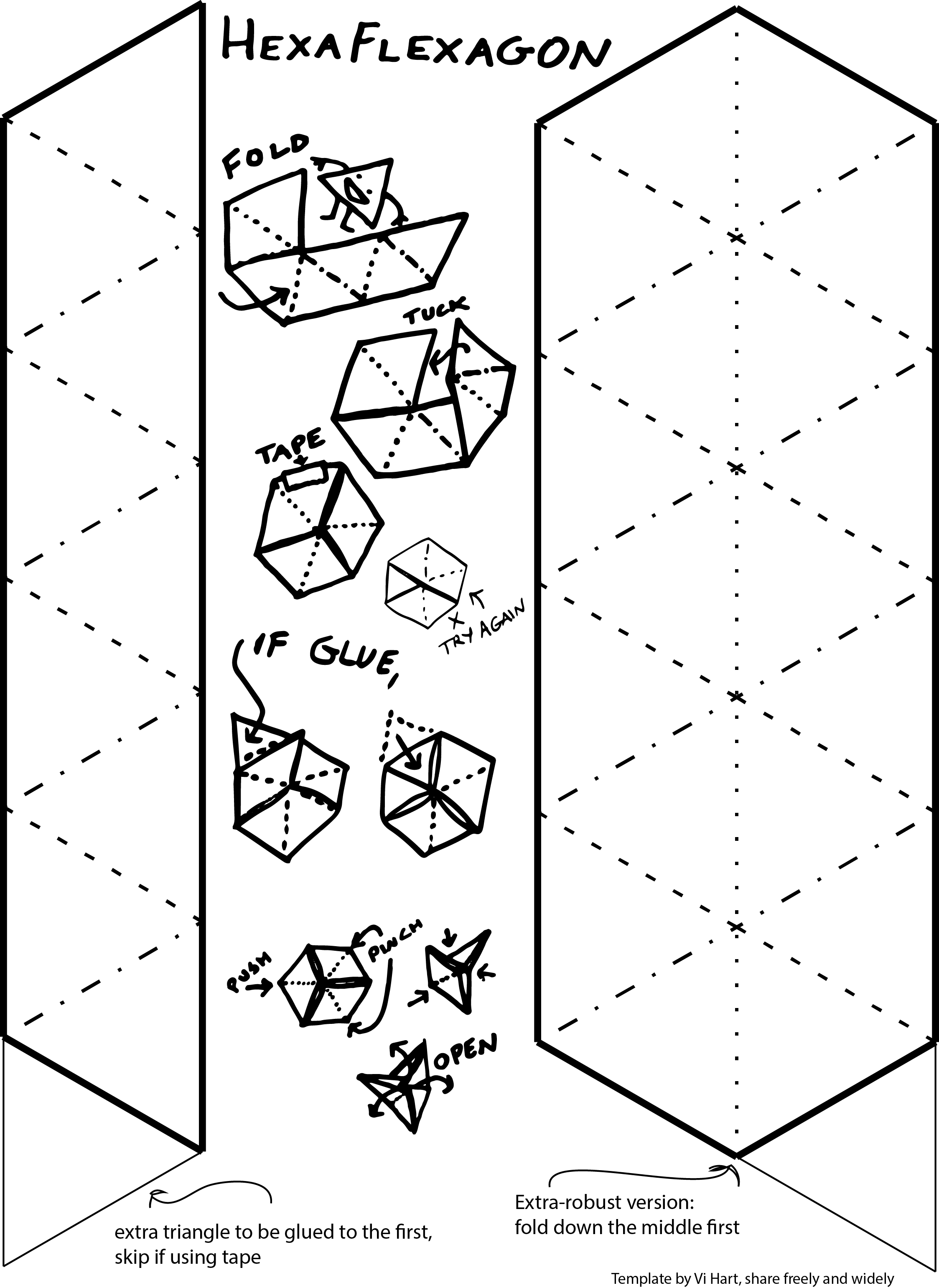
(my version coming soon :D)
also sorry idk how to center iframes
5/16/23 update: centered them! that took a bit